Many calculus survivors are left with nagging questions that haunt them their entire lives. While many turn to their therapists or religious leaders for answers, my niece searched at her uncle’s table. Now, though I am not a mathematician by profession, as I use mathematics to solve real-world problems, I happened to be available at the moment she began her existential search. “Shlomo, what is calculus used for anyway?” I began to wax poetically about all the myriad applications of integration and derivation. Suddenly, she interrupted my soliloquy with the real dagger she had been secreting in her cloak: “What possible use could you have had for the cross-product?” Unfortunately for dear Shaindy, her thrust was parried by a serendipitous act of providence: we had just used the cross-product in our development just that week.
As I have lamented numerous times in the past, one of the most challenging parts of my job is explaining to the business side why tasks they find trivial, so trivial that they are almost unnoticeable, are difficult for a mechanized being. One such task is page segmentation. When a human looks at a page of text, they can adroitly identify where paragraphs start and end, where the tables and forms are on a page, and which text is in which cell. Yet for a computer, life is a bit more complicated. Vision, a sense that we take for granted, is actually a really complex task for a computer. All the computer gets as input are numerical values, and from these it needs to reconstruct the immensely rich complexity of color, form, shape, and function. To illustrate my point, I will stick to a relatively simple application that we worked on recently: extracting text from forms.
Let’s begin by breaking down the process into simple steps:
- Identifying the form on the page.
- Segmenting the form into its cells.
- Extracting the text from each cell.
- Identifying some logical ordering for the cell texts.
These steps give us a list of tasks, each of which needs to be dealt with separately.
Let us begin with the identification problem: how can the computer identify the form on the page? There are a variety of approaches to this problem:
- Deep Learning: train a model on a lot of images containing forms (ex. cats, cars); have the computer identify and confirm their existence, and then extract their location.
- Classical Computer Vision: Identify lines using a line detection algorithm ( e.g. Canny Edge Detection) and use the lines to reconstruct the position of a table.
These approaches each come with their trade-offs. Therefore, different practitioners, based on various considerations, choose different paths. We chose to attack this problem using the classical approach (after all, it is more fun. This plays more of a role in our decisions than we tell the business side). Using classical algorithms means that we need to solve the following subproblems (dizzy yet?):
- Find the lines.
- Filter out the lines that are not part of a table (they may be part of a character or a random crease on the page).
- Construct the boxes from the lines.
- Match the characters to their proper location.
- Do this all quickly.
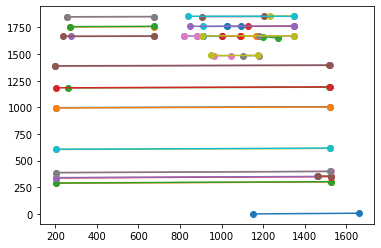
To find the lines (step 1), we use a line detection algorithm from the package OpenCV which is a multi-stage algorithm that finds all continuous streams of pixels in an image. Due to the often poor quality of our images, lines would often get segmented into separate pieces even when representing the same entity. Here is an example:
As you can see, this image is a collection of horizontal lines found in a form containing signature lines. The circles are the endpoints of the line plots given to us by the algorithm, yet there are often multiple on the same line. Thus, in order for us to begin searching for boxes, we first need to merge the fragments into their ‘true’ lines and make sure that we are not merging two lines accidentally.
Once we have the correct lines, our next challenge is to find all the lines that intersect each other. Here my dear niece’s boogeyman, the cross-product, enters the fray. The cross-product of two vectors is a binary operation defined on vectors, which among other things, gives you the orientation of the vectors in a plane. While I will leave the technical details of this mathematical beauty to our under-appreciated mathematics teachers, I will delve a bit into one of its applications: finding whether two segments intersect in a plane.
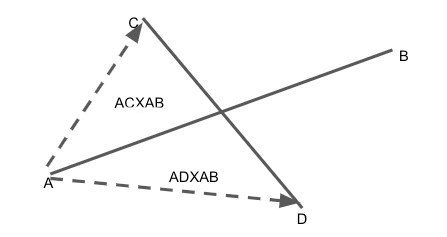
Consider the following image:
Here we have two lines, AB and CD, and we would like to check if they intersect. If we take the inner product of AB with an imaginary line AC and the inner product of AB with AD, if C and D lie on opposite sides of AB, the inner products will have opposite signs. If you repeat this check from the other direction, you can verify that the lines intersect.
Using this, we can find for each line, which lines intersect it. Once we have this list of all the lines with their intersections, we can construct all the boxes on the page with the simple observation that if A is intersected by B and C, and B and C are then intersected by D, we have a box made up of lines ABCD.
Now that we have completed steps 1-3, and in the process assuaged the angst of dear Shaindy about the utility of cross-products, we will take our leave. The rest of our approach requires a detailed dive into the concepts of delta lattices and Voronoi Diagrams, which would bore our most devoted reader (even you Babushka).
So I will conclude with a message to all the people afflicted with mathematical trauma who are still tortured by the seeming meaninglessness of what they went through. Do not turn to the bottle; do not despair and go off to pursue a liberal arts education. Find your local applied mathematician and speak with him/her and they may help you understand that you have absorbed an invaluable skill that will only get more important and valuable to you the more you believe in it. When you see the power, when you see the beauty through their eyes, whatever path you choose, you will understand that your life is all the better for calculus.